This is Adam and I am going to be your scribe for today.
First, I am going to show you how to write the equation of a transformed function graph.
Here's an example:
We are given a function f(x) and its transformation g(x), and we have to determine g(x)'s equation in the form 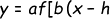]+k) .
.
First, we write down the corresponding coordinates of each function.
For now, we'll just leave this alone for the time being.
We have to figure out the stretches/compressions before we figure the translations so we start with our a (vertical) and b (horizontal) values. For the a values, we find the distance between the vertical points at the ends of each function.
If we divide g(x)'s vertical distance (4) by f(x)'s vertical distance (8), we get g(x)'s a value, which is  .
.
For the b values, we find the distance between the horizontal points at the ends of each function.
If we divide g(x)'s horizontal distance (8) by f(x)'s horizontal distance (2), we get g(x)'s b value, which is 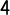 .
.

The b value is read as opposite or inverse, so the actual b value is 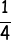 .
.
Now back to our coordinates. We have to figure out the h and k values, which can be difficult because the graph has been stretched horizontally and vertically. But we can get these points by applying the a and b values to the coordinate points of f(x).
Note that these points will turn into our g(x) values and we can find our h and k values through them.
We can find our h and k values by subtracting the x and y values in g(x) from the the x and y values in the coordinates we just calculated.
Keep in mind that the h value is read as opposite.
Finally, we plug in our a, b, h, and k values to get our final equation.
Here's a different example of how to find an Inverse of a Relation.
Graph the function =\frac{5}{3}x+2) and its inverse and determine the equation of
and its inverse and determine the equation of ) algebraically.
algebraically.
Before we graph it, we'll figure out how to find the inverse of a function.
First, you replace ) with
with 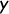 .
.
Secondly, you switch 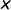 and
and 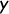 in the formula.
in the formula.
Thirdly, solve for 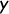 .
.
Finally, replace 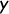 with
with ) .
.
Now, we can graph both functions at once based on our knowledge of linear functions. Note that each function reflects off each other on the y=x line, and that each coordinate of the original function is flipped in the inverse function.
Let's look at one final example for the Inverse of a Function.
Given =-(x-2)^2) , graph the function and the inverse, and show how the domain of
, graph the function and the inverse, and show how the domain of ) could be restricted so that
could be restricted so that ) is a function.
is a function.
First, we graph the quadratic function and write down the points so we can find the inverse easier.
To find the inverse using the points, just switch the x and y values and graph it.
To restrict the domain, you have to keep only one side of the function as having the full function will not pass the Horizontal Line Test (each y value will have two x values).
So instead of: 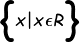
You can either have values less than the axis of symmetry (which is 2): 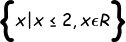
Or you can have values more than the axis of symmetry: 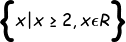
Aight, that's my blog. But you probably won't read it anyway








No comments:
Post a Comment