Remainder Theorem:
The Remainder Theorem is useful for evaluating polynomials at a given value of x.
The Remainder Theorem starts with an unnamed polynomial p(x), where "p(x)" that means "some polynomial p whose variable is x". Then dividing that polynomial by a linear factor x – a, where a is just some number. As a result of the synthetic division, you end up with some polynomial answer q(x) (the "q" standing for "the quotient polynomial") and some polynomial remainder r(x).
Example:
p(x) = x3 – 7x – 6 and divide be x-4( so a =4)

We get a quotient of q(x) = x2 + 4x + 9 , with a remainder of r(x) = 30.
If p(x) / (x – a) = q(x) with remainder r(x),
then p(x) = (x – a) q(x) + r(x).
Since (x^3 – 7x – 6) / (x – 4) = x2 + 4x + 9 with remainder 30,
then x3 – 7x – 6 = (x – 4) (x2 + 4x + 9) + 30.
Another way to get the remainder is we replace x with 4.
p(4) = (4 – 4)((4)2 + 4(4) + 9) + 30 = (0)(16 + 16 + 9) + 30 = 0 + 30 = 30
Factor Theorem:
The factor theorem is a theorem commonly applied to factorizing and finding the roots of polynomial equations. If P(x), a polynomial in x is divided by x - a and the remainder is zero, then (x - a) is a factor of P(x)
Example:
Is x - 2 is a factor of x2 - 7x + 10.
Let P(x) = x2 - 7x + 10
By the factor theorem, x - 2 is the factor of P(x) if P(2) = 0.
P(x) = x2 - 7x + 10
P(2) = 22 - 7 * 2 + 10 (Substitute x = 2)
= 4 - 14 + 10
= 0
Since P(2) = 0 => x - 2 is a factor of P(x).
Rational Root Theorem:
Steps to solving rational root theorem questions:
- Arrange the polynomial in descending order
- Write down all the factors of the constant term. These are all the possible values of p .
- Write down all the factors of the leading coefficient. These are all the possible values of q .
- Write down all the possible values of
 . Remember that since
factors can be negative,
. Remember that since
factors can be negative,
 and
-
and
-  must both be included.
Simplify each value and cross out any duplicates.
must both be included.
Simplify each value and cross out any duplicates.
 for which
P(
for which
P( ) = 0
. These are all the rational roots of
P(x)
.
) = 0
. These are all the rational roots of
P(x)
. Example:
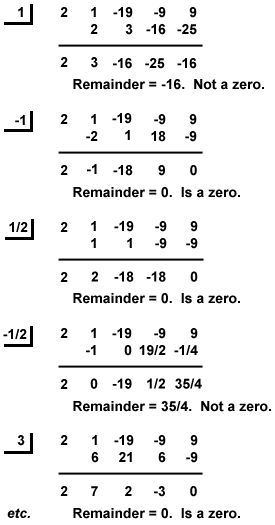
- P(x) = 2x 4 + x 3 -19x 2 - 9x + 9
- Factors of constant term: ±1 , ±3 , ±9 .
- Factors of leading coefficient: ±1 , ±2 .
- Possible values of
 :
±
:
±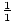 ,
±
,
±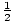 ,
±
,
±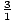 ,
±
,
±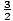 ,
±
,
±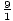 ,
±
,
±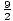 .
These can be simplified to:
±1
,
±
.
These can be simplified to:
±1
,
±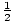 ,
±3
,
±
,
±3
,
±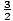 ,
±9
,
±
,
±9
,
±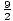 .
.
- Use synthetic division:
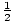 , and
3
.
, and
3
.Sources:
http://www.purplemath.com/modules/remaindr.htm
http://math.tutorvista.com/algebra/factor-theorem.html
http://www.sparknotes.com/math/algebra2/polynomials/section4.rhtml
No comments:
Post a Comment