Reflections and Stretches

Hii guys
this is a blog about our lesson on reflections and stretches

Reflections:
There are two types of reflections, the reflection over the x-axis and the reflection over the y-axis.

• The reflection over x-axis, makes the y values negative
• The reflection over y-axis, makes the x values negative

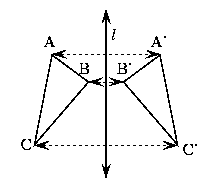
Can A Mirror Line Be Vertical? Yes.

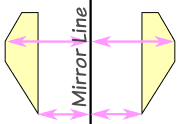
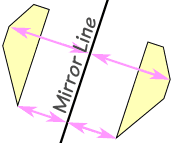
In fact Mirror Lines can be in any direction. Imagine turning the photo at the top in different directions ... ... the reflected image is always the same size, it just faces the other way:

A reflection is a flip over a line

Reflection Transformation: Example 1

The coordinates of LMNO are: (-7,5); (0,5); (-2,1); (-5,1) LMNO is reflected over the X-axis making the coordinates of L1M1N1O1: (-7,-5); (0,-5); (-2,-1); (-5,-1) Note how the x-coordinates remain the same but the y-coordinates change to their opposite integer (i.e. the sign changes). This is always the case with reflections over the X-axis.

Reflection Transformation: Example 2

The coordinates of PQSR are: (-8,-3); (-2,-3); (-2,-6); (-8,-6) PQSR is reflected over the Y-axis making the coordinates of P1Q1S1R1: (8,-3); (2,-3); (2,-6); (8,-6) Note how the y-coordinates remain the same but the x-coordinates change to their opposite integer (i.e. the sign changes). This is always the case with reflections over the Y-axis.

y = -f(x)	Reflects it about x-axis
y = f(-x)	Reflects it about y-axis

y = -f(x) makes y opposite

y = f(-x) makes x opposite

what is the reflected ordered pair if  (5,-2) is reflected on both axis

• x-axis (5,-2) -> (5,2)
• y-axis (5,-2) -> (-5,-2)

OR

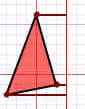
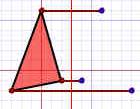
1. Measure from the point to the mirror line

2. Measure the same distance again on the other side and place a dot.

3. Then connect the new dots up!

1.)                    2.)                 3.)

Stretches:

There are two types of stretches: the vertical stretches and the horizontal stretches

Vertical stretches:

y= af(x) and y= 1/af(x) stretches the entire graph vertically by a factor of |a| units.

~The coordinates of the points (x,y) translates to (x,ay) and (x,1/ay). The value of x does not change.

Horizontal stretches:

y= f(b x)b and y= f (1/b x) stretches the entire graph horizontally  by a factor of |b| units

~the coordinates of the point  change to (x,y) to (1/b x, y) and (bx,y). The  value of y does not change.

• f(x)= f(2x)

multiply x values by 1/2 or divide by 2

• f(x)= f (1/2x)

multiply x values by 2 or divide by 1/2

example:

The graph of f(x) = 2 sin 2x is a stretch of sin x by scale factor 2 in the y-axis, and a stretch scale factor 1/a in the x-axis.

f(x) = sin x

The original function...

f(x) = 2 sin x

Stretches the original function in the y axis...

Horizontal Stretch A horizontal stretching is the stretching of the graph away from the y-axis.  A horizontal compression is the squeezing of the graph towards the y-axis.If the original (parent) function is y = f (x), the horizontal stretching or compressing of the function is the function f (ax). if 0 < a < 1 (a fraction), the graph isstretched horizontally by a factor of a units.

if a > 1, the graph is compressed horizontally by a factor of a units. if a should be negative, the horizontal compression or horizontal stretching of the graph is followed by a reflection of the graph across the y-axis. Vertical Stretch A vertical stretching is the stretching of the graph away from the x-axis. A vertical compression is the squeezing of the graph towards the x-axis.If the original (parent) function is y = f (x), the vertical stretching or compressing of the function is the function a f(x). if 0 < a < 1 (a fraction), the graph iscompressed vertically by a factor of a units. if a > 1, the graph is stretched verticallyby a factor of a units. If a should be negative, then the vertical compression or vertical stretching of the graph is followed by a reflection across the x-axis.

End =)

Sources:

• http://www.biology.arizona.edu/biomath/tutorials/transformations/reflections.html
• http://www.mathsisfun.com/sets/function-transformations.html
• http://www.regentsprep.org/Regents/math/algtrig/ATP9/funclesson1.htm