Hello! I found some additional information about Combinations and also some tips for Permutations.
Combinations and Permutations
What's the Difference?
In English we use the word "combination" loosely, without thinking if the order of things is important. In other words:
| "My fruit salad is a combination of apples, grapes and bananas" We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad. | |
| "The combination to the safe was 472". Now we do care about the order. "724" would not work, nor would "247". It has to be exactly 4-7-2. |
So, in Mathematics we use more precise language:
| If the order doesn't matter, it is a Combination. | |
| If the order does matter it is a Permutation. |
 | So, we should really call this a "Permutation Lock"! |
In other words:
A Permutation is an ordered Combination.
Combinations
There are also two types of combinations (remember the order does not matter now):
- Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
- No Repetition: such as lottery numbers (2,14,15,27,30,33)
1. Combinations with Repetition
Actually, these are the hardest to explain, so I will come back to this later.
2. Combinations without Repetition
This is how lotteries work. The numbers are drawn one at a time, and if you have the lucky numbers (no matter what order) you win!
The easiest way to explain it is to:
- assume that the order does matter (ie permutations),
- then alter it so the order does not matter.
Going back to our pool ball example, let us say that you just want to know which 3 pool balls were chosen, not the order.
We already know that 3 out of 16 gave us 3,360 permutations.
But many of those will be the same to us now, because we don't care what order!
For example, let us say balls 1, 2 and 3 were chosen. These are the possibilites:
| Order does matter | Order doesn't matter |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
So, the permutations will have 6 times as many possibilites.
In fact there is an easy way to work out how many ways "1 2 3" could be placed in order, and we have already talked about it. The answer is:
3! = 3 × 2 × 1 = 6
(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)
So, all we need to do is adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren't interested in the order any more):
That formula is so important it is often just written in big parentheses like this:
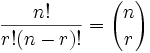 |
| where n is the number of things to choose from, and you choose r of them (No repetition, order doesn't matter) |
Here are some tips that can help you in permutations:
Tip #1
0! = 1Tip #2
Factorials of negative integers and fractions are not defined.Tip #3
Tip #4
Tip #5
The number of permutations of n distinct objects taken all at a time is n!.Tip #6
Tip #7
Tip #8
Tip #9
Tip #10

Tip #11
Number of circular permutations of n different things taken all at a time = (n-1)! (If clockwise and anticlockwise orders are taken as different).Tip #12

Tip #13
In permutation order of objects is important whereas in combination order of objects is not important.Tip #14
If m = n, then groups are of equal size. Division of these groups can be given by two types.Tip #15

Here are some additional problems that you can practice for combinations:
http://www.youtube.com/watch?v=oQpKtm5TtxU
http://www.youtube.com/watch?v=v9NLtiVt3XY
http://www.youtube.com/watch?v=SbpoyXTpC84
http://www.youtube.com/watch?v=DIjlllgq3dc
Source:
GOOGLE! :D
http://www.mathsisfun.com/combinatorics/combinations-permutations.html
http://www.simplylearnt.com/tips-tricks/Permutation-and-Combination
No comments:
Post a Comment