Binomial Theorem

Write a Blog?

 

Binomial Theorem

What happens when you multiply a binomial by itself ... many times?
BINOMIAL-CEPTION

 

 

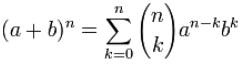
What is a Binomial?

A binomial is a polynomial with two terms.

Multiplying

The Binomial Theorem shows what happens when you multiply a binomial by itself (as many times as you want).
It works because there is a pattern ... let us see if we can discover it.

Exponents of (a+b)

Now on to the binomial.

We will use the simple binomial a+b, but it could be any binomial.

Let us start with an exponent of 0 and build upwards.

Exponent of 0

When an exponent is 0, you get 1:

(a+b)⁰ = 1

Exponent of 1

When the exponent is 1, you get the original value, unchanged:

(a+b)¹ = a+b

Exponent of 2

An exponent of 2 means to multiply by itself:

(a+b)² = (a+b)(a+b) = a² + 2ab + b²

Exponent of 3

For an exponent of 3 just multiply again:

(a+b)³ = (a+b)(a² + 2ab + b²) = a³ + 3a²b + 3ab² + b³

 

^{GETTING SMARTER}

 ^{We have enough now to start talking about the pattern.}

The Pattern

In the last result we got:

a³ + 3a²b + 3ab² + b³

Now, notice the exponents of a. They start at 3 and go down: 3, 2, 1, 0: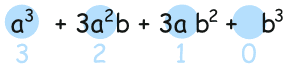

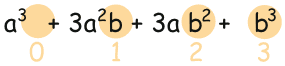
Likewise the exponents of b go upwards: 0, 1, 2, 3:

If we number the terms 0 to n, we get this:

k=0	k=1	k=2	k=3
a3	a2	a	1
1	b	b2	b3

Which can be brought together into this:

a^n-kb^k

  

Coefficients

So far we have:	a3 + a2b + ab2 + b3
But we really need:	a3 + 3a2b + 3ab2 + b3

We are missing the numbers (which are called coefficients).
Let's look at all the results we got before, from (a+b)⁰ up to (a+b)³:

And now look at just the coefficients (with a "1" where a coefficient wasn't shown):

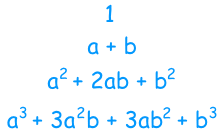
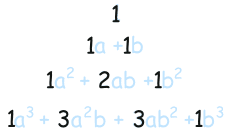
THIS MAKES PASCAL'S TRIANGLE

The Original Triangle

As a Formula

Our last step is to write it all as a formula.
But hang on, how do we write a formula for "find the coefficient from Pascal's Triangle" ... ?
Well, there is such a formula:

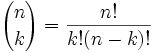It is commonly called "n choose k" because it is how many ways to choose k elements from a set of n.

Putting It All Together

The last step is to put all the terms together into one formula.
But we are adding lots of terms together ... can that be done using one formula?
Yes! The handy Sigma Notation allows us to sum up as many terms as we want:

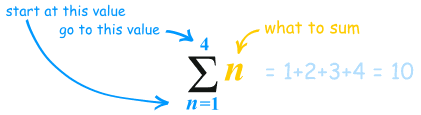
Sigma Notation

Now it can all go into one formula:

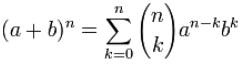
The Binomial Theorem

 

Sources:

Google: https://www.google.ca/

Math is Fun: http://www.mathsisfun.com/algebra/binomial-theorem.html